Workshop on Recent advances in stochastic algorithms
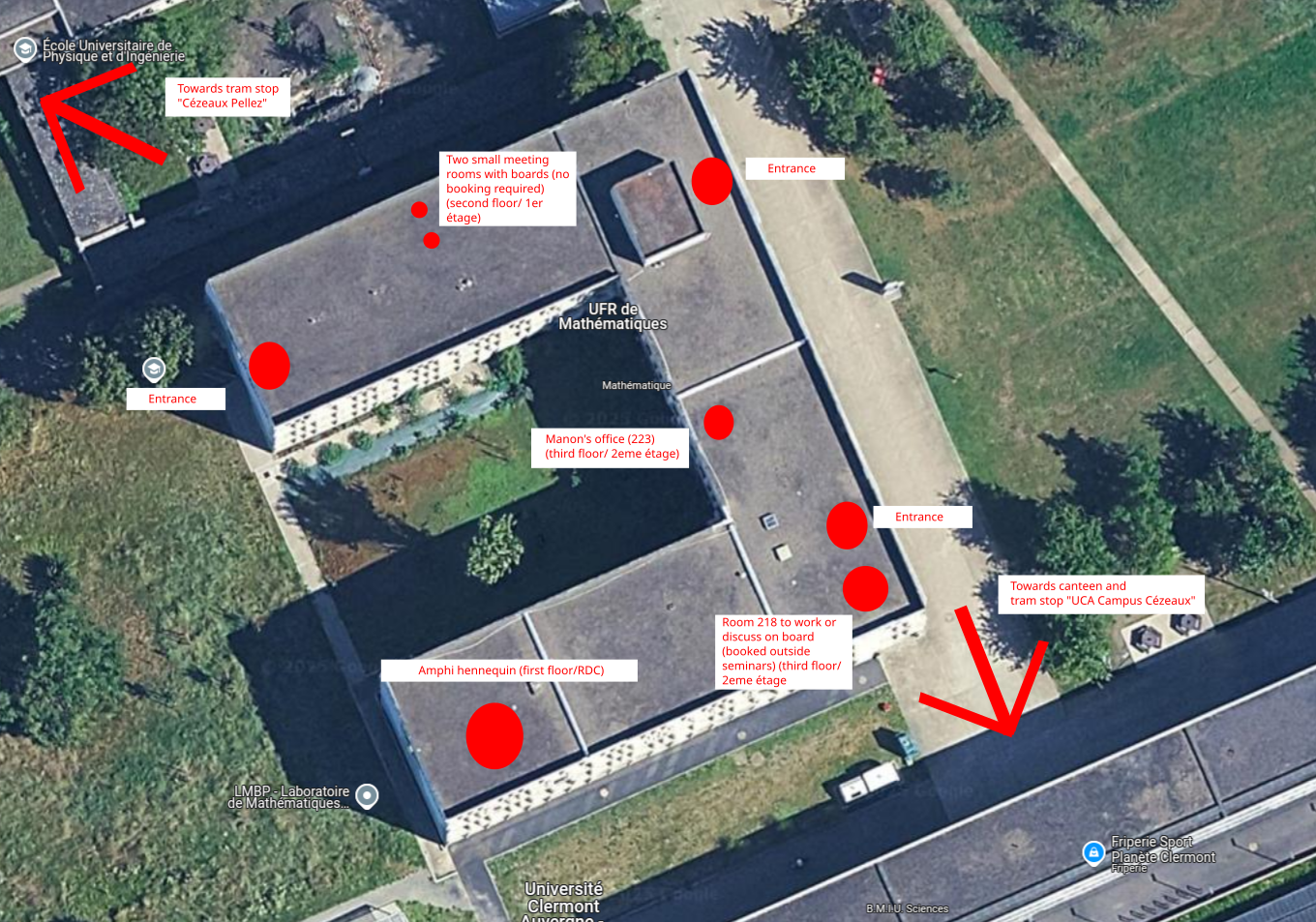
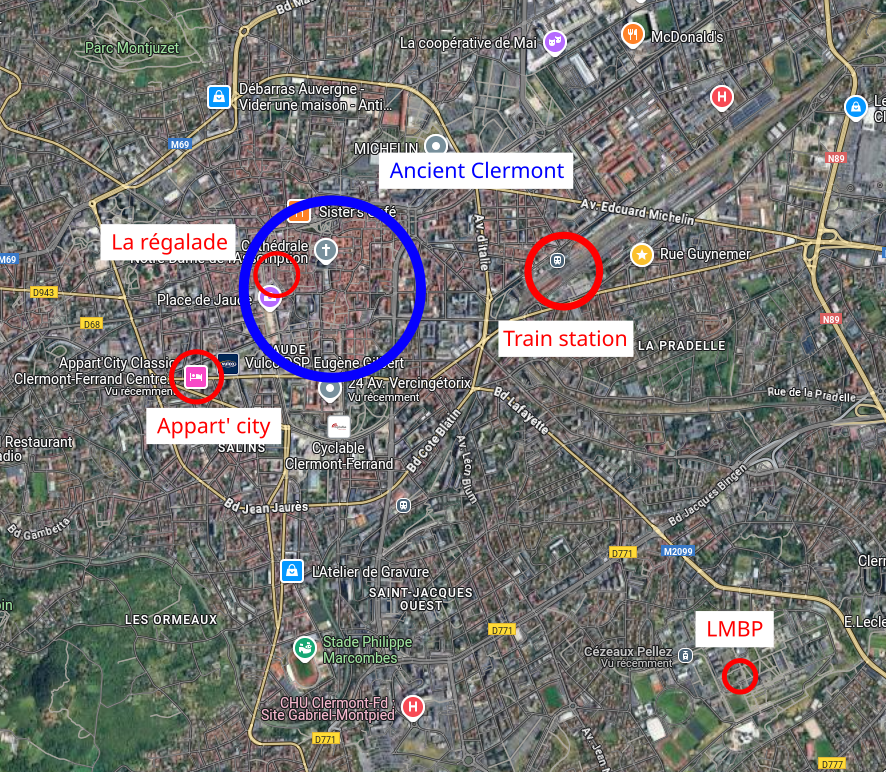
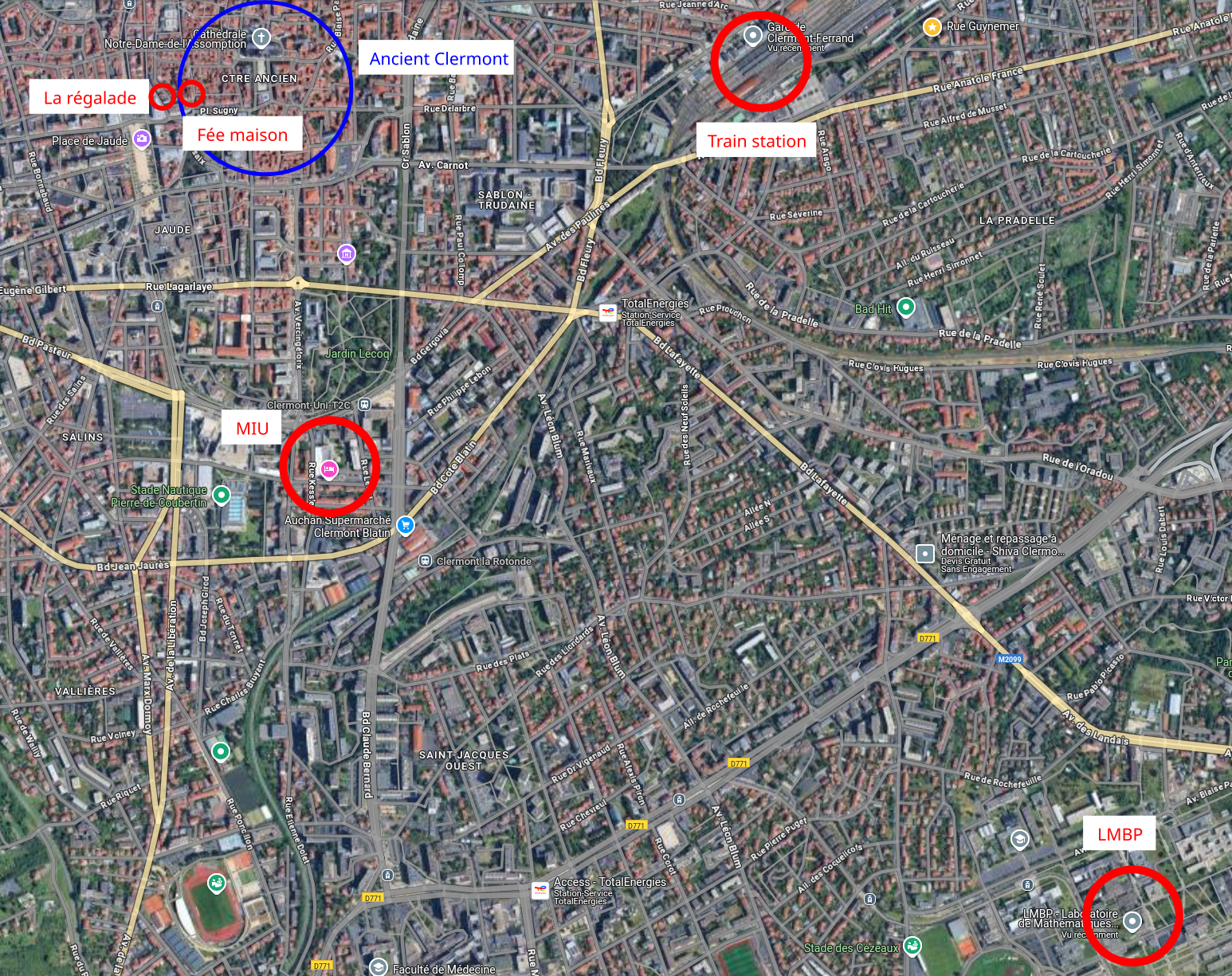
LMBP - Amphithéâtre Hennequin (first floor), Université Clermont Auvergne , July 8th-10th 2025
Organizer: Please contact Manon Michel (LMBP, Université Clermont Auvergne) for any inquiry.
Workshop booklet: Available here
Participants (click on title for abstract):
- Eddie Aamari (ENS Paris)
Generative diffusions and minimax estimation
The aim of this talk is to introduce generative models based on diffusions. After a brief reminder of the key concepts of stochastic calculus, we’ll detail how a time-reversed Ornstein-Uhlenbeck process can be used to transport distributions when starting from a Gaussian source. As this reversed process involves the so-called score function, we will then address the question of score learning via the minimization of an empirical contrast. Finally, we’ll discuss the stability of such a method, as well as minimax estimation speeds if time permits. Notes are available here.
- Yago Aguado (Université Clermont Auvergne)
- Marcelo Domingues (Université Clermont Auvergne)
- Florence Forbes (INRIA Grenoble)
Scalable Bayesian Experimental Design with Diffusions
Bayesian Optimal Experimental Design (BOED) is a powerful tool to reduce the cost of running a sequence of experiments. When based on the Expected Information Gain (EIG), design optimization corresponds to the maximization of some intractable expected contrast between prior and posterior distributions. Scaling this maximization to high dimensional and complex settings has been an issue due to BOED inherent computational complexity. In this work, we introduce a pooled posterior distribution with cost-effective sampling properties and provide a tractable access to the EIG contrast maximization via a new EIG gradient expression. Diffusion-based samplers are used to compute the dynamics of the pooled posterior and ideas from bi-level optimization are leveraged to derive an efficient joint sampling-optimization loop. The resulting efficiency gain allows to extend BOED to the well-tested generative capabilities of diffusion models. By incorporating generative models into the BOED framework, we expand its scope and its use in scenarios that were previously impractical. Numerical experiments and comparison with state-of-the-art methods show the potential of the approach.
- Cédric Gerbelot (ENS Lyon)
High-dimensional optimization for the multi-spike tensor PCA problem
A core difficulty in modern machine learning is to understand the convergence of gradient based methods in random, high-dimensional, non-convex landscapes. In this work, we study the behavior of gradient flow, Langevin dynamics and online stochastic gradient descent applied to the multi-spike tensor PCA problem, the goal of which is to recover a set of spikes from noisy observations of the corresponding tensor. The main thrust of our proof relies on a sharp control of the random part of the dynamics, followed by the analysis of a finite dimensional dynamical system, leading to both sample complexity bounds and a complete description of the set of critical points reached by the dynamics. In particular, we obtain sufficient conditions for reaching the global minimizer of the problem from uninformative initializations. At a technical level, we will put our methods, originating in probability and mathematical physics, in perspective with those used in machine learning theory and statistical physics of learning. This talk is based on joint work with Vanessa Piccolo and Gérard Ben Arous.
- Arnaud Guillin (Université Clermont Auvergne)
Lift and Flow Poincare for convergence of irreversible Markov processes
Non reversible Markov processes are usually known to be quicker to converge to equilibrium than reversible ones when targeting the same invariant measure. However, to get a quantitative statement is far from easy… we will adopt a lifting strategy to compare irreversible process such as underdamped Langevin, or stochastic algorithms, Bouncy Particle sampler, Zig-Zag or the Forward process. The approach is sufficiently general to handle physically relevant processes with subtle behaviors at boundaries.
(with A. Eberle, L. Hahn, F. Lorler and M. Michel)
- Sebastiano Grazzi (Bocconi University)
Parallel Computations for Metropolis Markov chains with Picard maps
In this talk, I will present parallel algorithms for simulating zeroth-order (aka gradient-free) Metropolis Markov chains based on the Picard map. For Random Walk Metropolis Markov chains targeting log-concave distributions pi on R^d, our algorithm generates samples close to pi in O(d^0.5) parallel iterations with O(d^0.5) processors, therefore speeding up the convergence of the corresponding sequential implementation by a factor O(d^0.5). Furthermore, a modification of our algorithm generates samples from an approximate measure pi_epsilon in O(1) parallel iterations and O(d) processors. We empirically assess the performance of the proposed algorithms in high-dimensional regression problems and an epidemic model where the gradient is unavailable. This is joint work with Giacomo Zanella.
- Pierre Jacob (ESSEC)
Some progress on unbiased MCMC
Unbiased MCMC methods refer to algorithms that deliver unbiased estimators of posterior expectations. Proposed first by Peter Glynn and Chang-Han Rhee in 2014, these methods employ pairs of Markov chains that 1) marginally evolve as prescribed by an MCMC algorithm and 2) are jointly dependent in such a way that the chains coincide at a random meeting time. Designing such couplings is not obvious, but the reward, namely unbiased estimators, is appealing: it addresses both the difficulty of assessing the convergence of Markov chains, and the difficulty of using parallel processors for MCMC. This talk reviews these techniques, assuming little familiarity with classical MCMC algorithms and none with coupling methods. The last part of the talk will cover recent progress toward turning unbiased MCMC into a widely-applicable and powerful addition to the Monte Carlo computational toolbox.
- Benedict Leimkuhler (University of Edinburgh)
SamAdams: an adaptive stepsize Langevin sampling algorithm inspired by the Adam optimizer
Prelude: I will discuss the use of Langevin-style diffusions for ergodic approximation, some of the choices available in the design of numerical algorithms and the standard methods used for their analysis. I will also mention a few of the challenges in the area.
Main talk:I will present a framework for adaptive-stepsize MCMC sampling based on time-rescaled Langevin dynamics, in which the stepsize variation is dynamically driven by an additional degree of freedom. The use of an auxiliary relaxation equation allows accumulation of a moving average of a local monitor function and while avoiding the need to modify the drift term in the physical system. Our algorithm is straightforward to implement and can be readily combined with any off-the-peg fixed-stepsize Langevin integrator. I will focus on a specific variant in which the stepsize is controlled by monitoring the norm of the log-posterior gradient, inspired by the Adam optimizer. As in Adam, the stepsize variation depends on the recent history of the gradient norm, which enhances stability and improves accuracy. I will discuss the application of our method to examples such as Neal’s funnel and a Bayesian neural network for classification of MNIST data. Joint work with Rene Lohmann (Edinburgh) and Peter Whalley (ETH).
The University of Edinburgh is a charitable body, registered in Scotland, with registration number SC005336. Is e buidheann carthannais a th’ ann an Oilthigh Dhùn Èideann, clàraichte an Alba, àireamh clàraidh SC005336.
- Pierre Latouche (Université Clermont Auvergne)
Importance weighted variational graph autoencoders for inference in deep latent position block models
In this presentation, I will first show how latent position models can be made compatible with block models for network analysis through the use of deep generative models. I will focus on the binary edge case and introduce a new random graph model along with a variational graph auto encoding strategy for inference. I will discuss the identifiability of the model and explain how model selection can be performed. I will then move to the sparse discrete edge case in the same deep, block compatible, modelling framework. I will show how importance weighted variational inference can strongly improve the inference procedure over the classical variational auto encoding strategy. I will give the importance weights used for sampling and show that, in the limit, the lower bound obtained converges to the integrated log likelihood of the data. Through this presentation, I will emphasise the need to rely on flexible random graph models to obtain relevant loss functions.
- Cyril Letrouit (Université Paris-Saclay)
Quantitative stability of optimal transport maps
Optimal transport consists in sending a given source probability measure rho to a given target probability measure 𝜇 in an optimal way with respect to a certain cost. On bounded subsets of R^d, if the cost is given by the squared Euclidean distance and if rho is absolutely continuous, there exists a unique optimal transport map from rho to mu. Optimal transport has been widely applied across various domains in statistics: for instance to compare distributions, for defining barycenters, to construct embeddings, in generative modeling, etc.
In this talk, we provide a quantitative answer to the following stability question: if mu is perturbed, can the optimal transport map from rho to mu change significantly? The answer depends on the properties of the density rho. This question takes its roots in numerical optimal transport, and has found applications to other problems like the statistical estimation of optimal transport maps, the random matching problem, or the computation of Wasserstein barycenters.
- Martin Metodiev (Université Clermont-Auvergne)
Easily Computed Marginal Likelihoods for Multivariate Mixture Models Using the THAMES Estimator
We present a new version of the truncated harmonic mean estimator (THAMES) for univariate or multivariate mixture models. The estimator computes the marginal likelihood from Markov chain Monte Carlo (MCMC) samples, is consistent, asymptotically normal and of finite variance. In addition, it is invariant to label switching, does not require posterior samples from hidden allocation vectors, and is easily approximated, even for an arbitrarily high number of components. Its computational efficiency is based on an asymptotically optimal ordering of the parameter space, which can in turn be used to provide useful visualisations. We test it in simulation settings where the true marginal likelihood is available analytically. It performs well against state-of-the-art competitors, even in multivariate settings with a high number of components. We demonstrate its utility for inference and model selection on univariate and multivariate data sets.
- Manon Michel (Université Clermont Auvergne)
- Martin Rouault (Université de Lille)
Monte Carlo methods with Gibbs measures
Monte Carlo methods such as MCMC are now routine in Bayesian machine learning, yet they come with slow convergence rates. Obtaining tight confidence intervals thus requires building estimators based on a big number of point which can be prohibitive in some applications where the likelihood of the Bayesian model is very expensive to evaluate. It is then desirable to obtain similar confidence intervals with a much smaller number of points, even it building those points is computationally more expensive. In this talk, I will first show how points jointly drawn from a Gibbs measure inspired by statistical physics can yield tighter confidence intervals than MCMC with the same number of points. Sampling points from this Gibbs measure however comes with practical issues since i) there is no known exact sampling algorithm, ii) it relies on the evaluation of untractable quantities. I will address the second issue and show that one can incorporate approximation of those untractable quantities without loss on the asymptotic confidence intervals.
Work in collaboration with Rémi Bardenet and Mylène Maïda.
- Andi Wang (Warwick University)
Explicit convergence rates of the underdamped Langevin diffusion under weight and weak Poincaré inequalities
I will discuss recent advances in obtaining convergence rates for the underdamped Langevin diffusion, the backbone of many non-reversible Monte Carlo methods. After reviewing the case of the reversible overdamped Langevin diffusion with light tails, I will discuss in more detail our recent work focussing on the case of heavy tailed targets in the non-reversible setting.
- Peter Whalley (ETH Zürich)
Scalable kinetic Langevin Monte Carlo methods for Bayesian inference
We introduce Langevin Monte Carlo methods for estimating expectations of observables under high-dimensional probability measures. We discuss discretization strategies and Metropolization methods for removing bias due to discretization error.
We then present a new unbiased method for Bayesian posterior means based on kinetic Langevin dynamics that combines advanced splitting methods with enhanced gradient approximations. Our approach avoids Metropolis correction by coupling Markov chains at different discretization levels in a multilevel Monte Carlo approach. Theoretical analysis demonstrates that our proposed estimator is unbiased, attains finite variance, and satisfies a central limit theorem. We prove similar results using both approximate and stochastic gradients and show that our method’s computational cost scales independently of the size of the dataset. Our numerical experiments demonstrate that our unbiased algorithm outperforms the “gold-standard” randomized Hamiltonian Monte Carlo.
We then discuss whether it is always necessary to remove discretization bias in high-dimensional models and applications of unadjusted MCMC algorithms in Bayesian Neural Network models.

Workshop on Longtime behaviors of stochastic processes
LMBP - Amphithéâtre Hennequin (first floor), Université Clermont Auvergne , June 2th-6th 2025
Organizer: Please contact Manon Michel (LMBP, Université Clermont Auvergne) for any inquiry.
Workshop booklet: Available here
Participants (click on title for abstract):
- Thibaut Arnoulx de Pirey (CEA Saclay)
Dynamical slowdown in high-dimensional population dynamics
I will discuss recent results on the long-time behavior of high-dimensional deterministic models of population dynamics. Using an exactly solvable model, I will show that dynamical slowdown generically arises due to the existence of many absorbing states (namely, if a population goes extinct, it remains extinct forever). In parallel, at long times, the steady-state measure is found to concentrate around unstable fixed points of the deterministic dynamics, the properties of which simple counting arguments on the ensemble of possible fixed points fail to account for. I will conclude the presentation by extending these results to more complex canonical models of population dynamics and by discussing possible connections to the dynamics of real-world high-diversity ecosystems.
- Yago Aguado (Université Clermont Auvergne)
- Camille Aron (ENS Paris, EPFL)
Slowing the butterflies: From stochastic resets in nonlinear maps to quenched disorder in metals
The spatiotemporal scrambling of information in chaotic many-body systems not only underpins the foundations of statistical physics but also presents significant challenges for the reliable operation of (quantum) information processing devices as system complexity increases. We demonstrate how key diagnostics of chaos—specifically, the Lyapunov exponent and the butterfly velocity—can be systematically suppressed by stochastically resetting dynamical systems to their initial conditions. Analogous to how the Navier–Stokes equations provide an effective description of fluid dynamics, we discuss the potential formulation of an effective field theory for information scrambling, capable of capturing the coarse-grained dynamics of information spreading in space and time. This perspective connects minimal nonlinear models, such as the logistic map, with more complex instances of interacting quantum systems, such as interacting diffusive metals.
- Christophe Bahadoran (Université Clermont Auvergne)
Invariant measures, hydrodynamics and relaxation limits for multilane exclusion processes
The totally asymmetric exclusion process (TASEP) is a fundamental stochastic model in nonequilibrium statistical physics, where particles with mutual exclusion hop on the doubly infinite 1d lattice subject to an external field . It is related to random polymers, queuing networks and growth models, as well as a simplified traffic-flow model. I will describe recent results on multilane exclusion processes, where exclusion processes on different lanes interact through lane changes:
i) The structure of invariant measures, which interpolates between known 1d results and conjectural multi-d results. ii) The hydrodynamic limit, i.e. the evolution of the macroscopic density field, with phase transitions related to lane competition. iii) Relaxation limits for the microscopic dynamics and related PDEs in the fast lane-change limit.
(Joint works with G. Amir, O. Busani and E. Saada)
References:
Invariant measures for multilane exclusion processe. To appear in Ann. Inst. Poincaré Probabilités et Statistique. ArXiv: 2105.12974
Hydrodynamics and relaxation limits for multilane exclusion processes and related hyperbolic systems. ArXiv: 2501.19355
- Tristan Benoist (Université Toulouse)
Long time behavior of quantum trajectories
Quantum trajectories are Markov processes modeling the evolution of a system subjected to repeated (indirect) measurement. The prototypical example of an experience they describe is Haroche’s group experiment measuring the number of photons in a superconducting cavity using Rydberg atoms. They are used on a daily basis in quantum optics. In this presentation I will review recent results on the longtime behavior of quantum trajectories. In particular I will detail the notion of « purification » central to these processes. I will explain how it is used to prove the uniqueness of the invariant measure, spectral gap and several related limit theorems.
- Richard Blythe (University of Edinburgh)
Cluster dynamics of dense interacting run-and-tumble particles in 1d
(with Peter Sollich, Martin Evans and Satya Majumdar)
Run-and-tumble particles (known also as persistent random walkers) exhibit a motion inspired by certain organisms (such as bacteria and fish), whereby particles seek to maintain a pre-determined speed in some direction, but change direction as a stochastic process. When such particles interact, for example through hard-core exclusion, detailed balance is broken and the statistical properties of dense systems defy a detailed understanding. In this talk I will summarise progress with the one-dimensional problem, focussing particularly on the dynamics of clusters that form in the limit where directional changes are rare. We show that these dynamics can be expressed as a coagulation-fragmentation process that in a continuum limit takes the form of an advection-diffusion equation. A particular challenge is that the advection coefficient is time-dependent. Despite this, we are able to gain some insights into the nature of the relaxation to stationarity, although a number of open problems remain.
- Benoît Dagallier (Université Paris-Dauphine)
Log-Sobolev inequalities for mean-field particle systems.
We consider the (overdamped) Langevin dynamics associated with particles interacting through a smooth mean-field potential and attempt to quantify its speed of convergence as a function of the number N of particles and the temperature. The main goal is to find a criterion relating fast convergence speed, i.e. independent of N, to properties of the static free energy of the model.
We show that a certain notion of convexity of the free energy implies uniform-in-N bounds on the convergence speed, measured through a log-Sobolev inequality. In some cases this convexity criterion is sharp, for instance in the Curie-Weiss model where convexity holds up to the critical temperature.
Our proof does not involve the dynamics. Instead, we decompose the measure describing interactions between particles with inspiration from renormalisation group arguments for lattice models, that we adapt here to a lattice-free setting in the simplest case of mean-field interactions. Our results apply more generally to non mean-field, possibly random settings, provided each particle interacts with sufficiently many others.
Based on joint work with Roland Bauerschmidt and Thierry Bodineau.
- Marcelo Domingues (Université Clermont Auvergne)
- Andreas Eberle (Universität Bonn)
Non-reversible lifts of reversible diffusion processes and relaxation times
We propose a new concept of lifts of reversible diffusion processes and show that various well-known non-reversible Markov processes arising in applications are lifts in this sense of simple reversible diffusions. Furthermore, we introduce a concept of non-asymptotic relaxation times and show that these can at most be reduced by a square root through lifting, generalising a related result in discrete time.
For reversible diffusions on domains in Euclidean space, or, more generally, on a Riemannian manifold with boundary, non-reversible lifts are in particular given by the Hamiltonian flow on the tangent bundle, interspersed with random velocity refreshments, or perturbed by Ornstein-Uhlenbeck noise, and reflected at the boundary. In order to prove that for certain choices of parameters, these lifts achieve the optimal square-root reduction up to a constant factor, precise upper bounds on relaxation times are required. We demonstrate how the recently developed approach to quantitative hypocoercivity based on space-time Poincaré inequalities can be rephrased and simplified in the language of lifts and how it can be applied to find optimal lifts.
This is joint work with Francis Lörler (Bonn).
- Max Fathi (Sorbonne Université)
The cutoff phenomenon: old and new
In this talk, I will discuss cutoff for Markov chains, a phenomenon where the profile of convergence to equilibrium for a sequence of Markov chains becomes more and more abrupt. I will present the context, and some recent developments by Justin Salez and his collaborators, based on functional inequalities and curvature. If time allows, I will discuss some recent work with Djalil Chafaï and Nikita Simonov on cutoff for nonlinear PDE, and a few open problems.
- Aurélien Grabsch (Sorbonne Université)
Tracer and current fluctuations in 1D diffusive systems
In this talk, I will review recent results obtained on the symmetric simple exclusion process (SEP) and other models of 1D diffusive systems. At large scales, these models can be studied within the framework of macroscopic fluctuation theory (MFT). For a few models, like the SEP, the MFT equations are classically integrable and can be solved to obtain exact results. However for most systems this is not the case, but several results can still be obtained in this case and applied to realistic models of interacting particles.
- Arnaud Guillin (Université Clermont Auvergne)
- Leo Hahn (Université de Neuchâtel)
Investigating the Shape Transition of Run-and-Tumble Particles: A One-Dimensional PDMP Approach to the Regularity of the Invariant Measure
The invariant measure of a wide class of run-and-tumble particles (RTPs) subjected to a potential possesses a density, which may be either continuous or discontinuous, depending on model parameters. This key feature, known as shape transition, indicates whether the system is close to equilibrium (continuous density) or substantially departs from it (discontinuous density). Building on and extending existing results concerning the regularity of the invariant measure of one-dimensional piecewise-deterministic Markov processes (PDMPs), I will show how to characterize the shape transition even in situations where the invariant measure cannot be computed explicitly. This analysis confirms shape transition as a robust, general feature of RTPs under a potential, and also refines the regularity theory for the invariant measure of one-dimensional PDMPs.
- Sophie Hermann (Sorbonne Université)
Noether’s theorem and hyperforces in statistical mechanics
Noether’s theorem is familiar to most physicists due its fundamental role in linking the existence of conservation laws to the underlying symmetries of a physical system. I will present how Noether’s reasoning also applies within statistical mechanics to thermal systems, where fluctuations are paramount. Exact identities (“sum rules”) follow thereby from functional symmetries. The obtained sum rules contain both, well-known relations, such as the first order term of the Yvon-Born-Green (YBG) hierarchy (i.e. the spatially resolved force balance), as well as previously unknown identities, relating different correlations in many-body systems. The identification of the underlying Noether concept enables their systematic derivation. Since Noether’s theorem is quite general it is possible to generalize to arbitrary thermodynamic observables. This generalization yields sum rules for hyperforces, i.e. the mean product between the considered observable and the relevant forces that act in the system. Simulations of a range of simple and complex liquids demonstrate the fundamental role of these correlation functions in the characterization of spatial structure, such as quantifying spatially inhomogeneous self-organization. Finally, we show that the considered phase-space-shifting is a gauge transformation in equilibrium statistical mechanics.
- Pierre Illien (Sorbonne Université)
Non-Gaussian density fluctuations in the Dean-Kawasaki equation
Computing analytically the n-point density correlations in systems of interacting particles is a long-standing problem of statistical physics, with a broad range of applications, from the interpretation of scattering experiments in simple liquids, to the understanding of their collective dynamics. For Brownian particles, i.e. with overdamped Langevin dynamics, the microscopic density obeys a stochastic evolution equation, known as the Dean-Kawasaki equation. In spite of the importance of this equation, its complexity makes it very difficult to analyze the statistics of the microscopic density beyond simple Gaussian approximations. In this work, resorting to a path-integral description of the stochastic dynamics and relying on the formalism of macroscopic fluctuation theory, we go beyond the usual linearization of the Dean-Kawasaki equation, and we compute perturbatively the three-point density correlation functions, in the limit of high-density and weak interactions between the particles. This exact result opens the way to using the Dean-Kawasaki beyond the simple Gaussian treatments, and could find applications to understand many fluctuation-related effects in soft and active matter systems.
- Tony Jin (Université Côte d’Azur)
An exact representation of the dynamics of quantum spin chains as classical stochastic processes with particle/antiparticle pairs.
Since the advent of quantum mechanics, classical probability interpretations have faced significant challenges. A notable issue arises with the emergence of negative probabilities when attempting to define the joint probability of non-commutative observables. In this talk, I will propose a resolution to this dilemma by introducing an exact representation of the dynamics of quantum spin chains using classical continuous-time Markov chains (CTMCs). These CTMCs effectively model the creation, annihilation, and propagation of pairs of classical particles and antiparticles. The quantum dynamics then emerges by averaging over various realizations of this classical process.
- Lucas Journel (Université Paris-Saclay)
Uniform convergence of the Fleming-Viot process for the sampling of quasi-stationary measures
The Fleming-Viot process is a mean-field particle system whose empirical measure is an estimator of the law of a Markov process conditioned on its survival (in a way that we will define). In this talk I will present how to show the convergence of this estimator at a rate independent of time, and get exponential concentration inequalities in a soft killing case.
It is based on a work with Mathias Rousset from Inria Rennes.
- Vivien Lecomte (Université Grenoble Alpes)
Generalized Kirchoff’s Current Law(s)
In 1847, Kirchoff derived laws governing stationary currents and potential in electrical circuits, encoding conservation laws. They can be expressed in a local form (fluxes balance at nodes of the networks), or in a global form (where they express linear dependences between currents). Interestingly, such settings can be generalized to Markov chains (the conservation now being that of probability), and they imply that the stationary state can be expressed as a normalized sum of weights of covering trees of the graph between states (through «Kirchhoff’s formula» a.k.a. Markov Chain Tree Theorem). I will show that, in such settings, a surprisingly simple relation comes as a consequence of these laws: a mutual linearity between currents (stating that any stationary current is an affine function of any other set of –independent enough– current).
(Chemical) reactions networks are a generalization of such systems, where the network between species is now described by a hypergraph. I will explain how one can formulate a generalization of Kirchoff’s Current Law applying to these, and describe the associated geometrical interpretation. Finally, an application to the problem of metabolic reconstruction in constrained-based models will be detailed.
Work based on collaborations with Sara Dal Cengio, Pedro Harunari, Matteo Polettini and Delphine Ropers.
- Pierre Lebris (IHES)
Uniform in time mean field limit in the metastable Curie-Weiss model
Some low temperature particle systems in mean-field interaction are ergodic with respect to a unique invariant measure, while their (non-linear) mean-field limit may possess several steady states. In particular, in such cases, propagation of chaos (i.e. the convergence of the particle system to its mean-field limit as n, the number of particles, goes to infinity) cannot hold uniformly in time since the long-time behaviors of the two processes are a priori incompatible. However, the particle system may be metastable, and the time needed to exit the basin of attraction of one of the steady states of its limit, and go to another, is exponentially (in n) long. Before this exit time, the particle system reaches a (quasi-)stationary distribution, which we expect to be a good approximation of the corresponding non-linear steady state.
The goal of this talk is to study a toy model, the Curie-Weiss model, and show uniform in time propagation of chaos of the particle system conditioned to keeping a positive mean.
Based on joint work with L. Journel (Université de Neuchâtel).
- Francis Lörler (Universität Bonn)
Convergence of non-reversible lifts via flow Poincaré inequality with application to self-repelling motion
Convergence to equilibrium of non-reversible Markov processes can be quantified via an extended Poincaré-type inequality in space and time, termed the flow Poincaré inequality. We demonstrate how such a flow Poincaré inequality can be obtained for a large class of processes using the framework of second-order lifts. The result can be applied to obtain quantitative convergence rates for an event chain algorithm for the harmonic chain, which is closely related to a discretisation of the self-repelling motion introduced by B. Tóth and W. Werner.
The talk is based on joint work with Andreas Eberle, Arnaud Guillin, Leo Hahn and Manon Michel.
- Kirone Mallick (CEA Saclay)
Some exact results on Quantum Walks
Quantum analogs of classical random walks have been defined in quantum information theory as a useful concept to implement algorithms. Due to interference effects, statistical properties of quantum walks can drastically differ from their classical counterparts, leading to much faster computations.
Quantum walks define naturally a quantum dynamical system to which the counterparts of many questions on classical random walks can be generalized; they provide an ideal framework to study analytically the interplay between statistical and quantum effects. We shall present some exact results on continuous-time quantum walks on a lattice, such as survival properties of quantum particles in the presence of traps, growth of a quantum population in the presence of a source, and quantum return probabilities (Loschmidt echoes).
- Manon Michel (Université Clermont Auvergne)
- Julien Reygner (École des Ponts ParisTech)
Local convergence rates for Wasserstein gradient flows and McKean-Vlasov equations with multiple stationary solutions
Non-linear versions of log-Sobolev inequalities, that link a free energy to its dissipation along the corresponding Wasserstein gradient flow (i.e. corresponds to Polyak-Lojasiewicz inequalities in this context), are known to provide global exponential long-time convergence to the free energy minimizers, and have been shown to hold in various contexts. However they cannot hold when the free energy admits critical points which are not global minimizers, which is for instance the case of the granular media equation in a double-well potential with quadratic attractive interaction at low temperature. This work addresses such cases, extending the general arguments when a log-Sobolev inequality only holds locally and, as an example, establishing such local inequalities for the granular media equation with quadratic interaction either in the one-dimensional symmetric double-well case or in higher dimension in the low temperature regime. The method provides quantitative convergence rates for initial conditions in a Wasserstein ball around the stationary solutions. The same analysis is carried out for the kinetic counterpart of the gradient flow, i.e. the corresponding Vlasov-Fokker-Planck equation. The local exponential convergence to stationary solutions for the mean-field equations, both elliptic and kinetic, is shown to induce for the corresponding particle systems a fast (i.e. uniform in the number or particles) decay of the particle system free energy toward the level of the non-linear limit. This is a joint work with Pierre Monmarché.
- Grégory Schehr (Sorbonne Université)
Large Deviations in Switching Diffusion: from Free Cumulants to Dynamical Transitions
We study the diffusion of a particle whose diffusion constant changes randomly over time. Specifically, it switches between values drawn from a given distribution at a fixed rate. Using a renewal approach, we derive exact expressions for the moments of the particle’s position at any finite time and for any distribution with well-defined moments. In the long-time limit, we show that the cumulants of the position grow linearly with time and are directly related to the free cumulants of the underlying distribution of diffusion constants. For specific cases, we analyze the large deviations of the particle’s position, revealing rich behaviors and dynamical transitions in the rate function.


Probabilistic sampling for physics: Finding needles in a field of high-dimensional haystacks
Institut Pascal - Université Paris-Saclay , September 4th-22th 2023

Event Website: https://indico.ijclab.in2p3.fr/event/9042/
Organizer: Thomas Swinburne (CINaM, CNRS, Aix-Marseille Université) and Manon Michel (LMBP, CNRS, Université Clermont Auvergne).
Scientific committee: Alain Durmus (École Polytechnique, Massy-Palaiseau), Virginie Ehrlacher (École des Ponts, Marne la Vallée), Guilhem Lavaux (IAP, Paris), Mihai-Cosmin Marinica (CEA, Saclay), Martin Weigel (TU Chemnitz)
Description
This 3-week meeting aims at gathering physicists and mathematicians working on stochastic sampling. The overall goal is to foster new interdisciplinary collaborations to answer the challenges encountered while sampling probability distributions presenting high-energy barriers and/or a large number of metastable states. Such challenges are faced by researchers working in a diverse range of fields in science, from fundamental problems in statistical mechanics to large-scale simulations of materials; in recent years significant progress has been made on several aspects, including:
- design of Markov processes which break free from a random-walk behavior,
- numerical methods for dimensionality reduction of input data,
- mode-hopping non-local moves by generative models,
- density region detection,
- and analytical derivations of robustness guarantees.
By bringing together established experts and early-career researchers across a wide range of disciplines we aim to find new synergies to answer important and general questions, including:
- How to associate fastest local mixing strategies with mode-hopping moves?
- What physics can we preserve and extract along the dynamics?
- How to build reduced representations that can detect previously unseen events or regions?
Workshop on Scaling in Piecewise Deterministic Markov Processes
LMBP - ROOM 218, Université Clermont Auvergne , March 6th-9th 2023
Organizer: Please contact Manon Michel (LMBP, Université Clermont Auvergne) for any inquiry.
Participants: Andreas Eberle (Bonn University), Francis Lörler (Bonn university), Katharina Schuh (TU Wien), Pierre Monmarché (Sorbonne Université), Arnaud Guillin (UCA), Léo Hahn (UCA), Manon Michel (UCA)
Probabilistic numerical approaches in the context of large-scale physics
LMBP - ROOM 218, Université Clermont Auvergne , June 28th 2022
Organizer: Please contact Manon Michel (LMBP, Université Clermont Auvergne) for any inquiry.
Speakers: David Hill (ISIMA/LIMOS, UCA), Jens Jasche (Stockholm University), Guilhem Lavaux (IAP, France), Athina Monemvassitis (LMBP, UCA) and Lars Röhrig (TU Dortmund and LPC, UCA)
Schedule (click on title for abstract)
9.00 AM - 9.50 AM Guilhem Lavaux
The Aquila program: cosmological inference with complicated datasets
Cosmology deals with the study of the universe as a singular physical object with specific global properties. Over the last century, scientists have tried to build a consistent picture of our universe from astronomical data sets. Unfortunately, those data sets are both incomplete and complicated to interpret.
Over the last ten years, new data assimilation techniques got developed and made possible through advances in statistics, computer science, and a significant increase in the quantity and quality of data. The Aquila consortium intends to push the scientific analysis of those data sets to the next level. I wish to provide a panorama of the activities of the Aquila consortium. I will present the specific challenges of cosmological datasets and some of our statistical modeling techniques: from “likelihood full” with the BORG algorithm (Bayesian Origin Reconstruction from Galaxies) to “implicit likelihood” methods that rely on the use of neural networks. Beyond pure cosmological inference, members of Aquila also validate results by correlating with other data sets. This phase of validation also sometimes provides additional constraints.
9.50 AM - 10.40 AM Jens Jasche
Large-scale Bayesian inference of cosmic structures in galaxy
surveys
The standard model of cosmology predicts a rich phenomenology to test the fundamental physics of the origin of cosmic structure, the accelerating cosmic expansion, and dark matter with next-generation galaxy surveys.
However, progress in the field critically depends on our ability to connect theory with observation and to infer relevant cosmological information from next-generation galaxy data. State-of-the-art data analysis methods focus on extracting only information from a limited number of statistical summaries but ignore significant information in the complex filamentary distribution of the three-dimensional cosmic matter field.
To go beyond classical approaches, I will present our Bayesian physical forward modeling approach aiming at extracting the full physical plausible information from cosmological large-scale structure data in this talk. Using a physics model of structure formation, the approach infers 3D initial conditions from which observed structures originate, maps non-linear density and velocity fields, and provides dynamic structure formation histories including a detailed treatment of uncertainties. A hierarchical Bayes approach paired with an efficient implementation of a Hamiltonian Monte Carlo sampler permits to account for various observational systematic effects while exploring a multi-million-dimensional parameter space. The method will be illustrated through various data applications providing an unprecedented view of the dynamic evolution of structures surrounding us. Inferred mass density fields are in agreement with and provide complementary information to gold-standard gravitational weak lensing and X-ray observations. I will discuss how using Bayesian forward modeling of the three-dimensional cosmic structure permits us to use the cosmic structure as a laboratory for fundamental physics and to gain insights into the cosmic origin, the dark matter, and dark energy phenomenology as well as the nature of gravity. Finally, I will outline a new program to use inferred posterior distributions and information-theoretic concepts to devise new algorithms for optimal acquisition of data and automated scientific discovery.
10.40 AM - 11.10 AM Coffee break
11.10 AM - 11.35 AM Athina Monemvassitis
On the implementation of discrete PDMP-based algorithms
Traditional Markov-chain Monte Carlo methods produce samples from a target probability density by exploring it through a reversible Markov chain. In most cases, this chain satisfies the detail balance condition thanks to the introduction of rejections. Lately, non-reversible algorithms based on continuous Piecewise deterministic Markov processes (PDMP) have been shown to improve the sampling efficiency. Those algorithms produce irreversible ballistic motion while ensuring the global balance by direction changes instead of rejections. Much more efficient than the historical Metropolis-Hastings algorithm, they however require either some upper bound of the gradient of the log of the probability density or knowledge on both its inverse and the zeros of its gradient. In case one does not have direct access to those quantities, a compromise is to discretize the continuous PDMP process, at the cost of introducing direction flips and diminishing the persistent nature of the dynamics. In this talk, after introducing some properties of the continuous PDMPs, I will present the discretization before showing some numerical preliminary results on its efficiency with respect to its continuous counterpart and the Metropolis-Hastings algorithm.
11.35 AM - 12.00 AM Lars Röhrig
The Bayesian Analysis Toolkit and applications Slides here .
This talk faces the main aspects and key features of the Bayesian Analysis Toolkit in julia (BAT.jl), a software package to perform Bayesian inference in the julia programming language. BAT.jl offers a variety of efficient and modular algorithms for sampling, optimization and integration to explore posterior distributions in high-dimensional parameter spaces. After giving an introduction to the main aspects and algorithms of BAT.jl, a use-case is presented to perform indirect searches for physics beyond the Standard Model.
12.00 AM - 12.50 AM David Hill
Stochastic Parallel Simulations, repeatability and reproducibility, what is possible?
Parallel stochastic simulations are too often presented as non-reproducible. However, anyone wishing to produce a computer science work of scientific quality must pay attention to the numerical reproducibility of his simulation results. The main purpose is to obtain at least the same scientific conclusions and when it’s possible the same numerical results. However significant differences can be observed in the results of parallel stochastic simulations if the practitioner fails to apply the best practices. Remembering that pseudo-random number generators are deterministic, it is often possible to reproduce the same numerical results for parallel stochastic simulations by implementing a rigorous method tested up to a billion threads. An interesting point for some practitioners is that method enables to check the parallel results with their sequential counterpart before scaling, thus gaining confidence in the proposed models. This talk will present the concepts of reproducibility and repeatability from an epistemological perspective, then the state of the art for parallel random numbers and the method previously mentioned will be exposed in the current context of high performance computing including silent errors impacting all top 500 machines, including the new Exascale supercomputer.
Workshop funded by the 80 prime project CosmoBayes, associated to SuSa.

On future synergies for stochastic and learning algorithms
CIRM , September 27th – October 1st 2021
Event Website: https://conferences.cirm-math.fr/2389.html
Organizers: Alain Durmus (CMLA, ENS Paris Saclay), Manon Michel (LMBP, Université Clermont Auvergne), Gareth Roberts (Department of statistics, Warwick University) and Lenka Zdeborova (Institut de Physique Théorique, CEA).
Scientific committee: Arnaud Guillin (LMBP, Université Clermont Auvergne), Rémi Monasson (LPENS, ENS Paris), Éric Moulines (CMAP, École Polytechnique), Judith Rousseau (Statistics department, Oxford University), Benjamin Wandelt (IAP; ILP; Flatiron Institute).
Description
This workshop intends to gather computational statisticians, applied mathematicians and theoretical and computational physicists, working on the development and analysis of stochastic and learning algorithms. All these different fields revolve indeed around a probabilistic modelling, either of physical systems or data points, which are then completely characterised by a probability distribution. In physics, given the number of interacting objects is high enough, the system properties can indeed be casted into a Boltzmann distribution, whose corresponding potential function describes the interactions between the objects. In statistics, Bayesian inference replaces standard point-estimates of the parameters by a full probability distribution, which allows to take into consideration a priori information on the problem, but at the cost of having to deal with high-dimensional integrals. The goal is to strengthen the already known connections but more importantly to create new ones around Monte Carlo methods, Bayesian machine learning, probabilistic modelling, inverse problems, uncertainty quantification and applications to large-scale datasets in physics and statistics.
Our goal is to bring people from the different communities to discuss the practical and theoretical problems they face and their own take on them. For that purpose, the conference will be organized around 4 tutorial lectures, invited talks and contributed talks.